uProve is a simple and easy-to-use program for building natural deduction proofs in propositional logic
Help > Tutorial
Tutorial
The sequent that should be proved in this tutorial is p -< q, ~q |- ~p.
Start uProve.
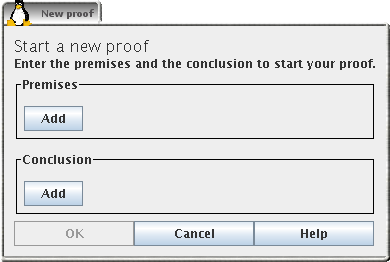
Select New... from the Proof menu.
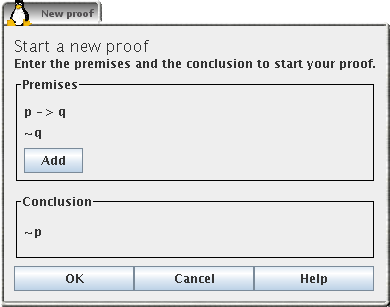
Enter the first premise
Click on the first Add button to open the dialog box for entering formulas.

Enter the second premise and the conclusion
Repeat the step above for the other two formulas too. The dialog should look like below when all three formulas are entered. Click OK to close the dialog and return to uProve's main window.
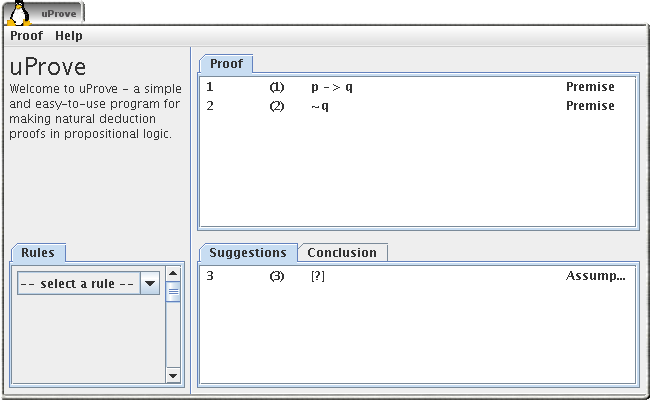
Assume p
The sequent in question is proved by doing a proof by contradiction, that is assuming the opposite of what we actually want and prove that we get a contradiction from that. Since ~p is what we want, we start by assuming p. An assumption is done by clicking on the only available line in the list of suggestions. A dialog is opened that lets us enter what we want to assume (p).

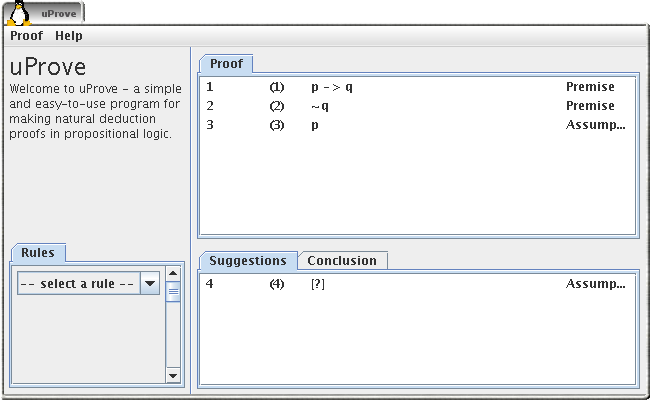
Apply an implication elimination
Our goal is now to get a contradiction. This can be done by using implication elimination on the first (p -> q) and the last (p) lines. Click on these two lines to select them. The list of suggestions is now updated. Click on the wanted implication elimination (third line from the top).
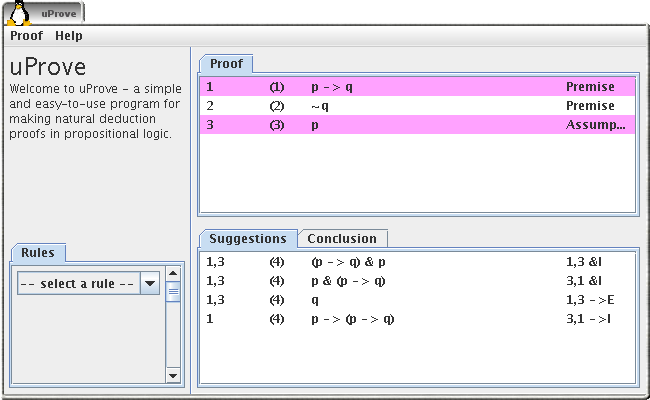
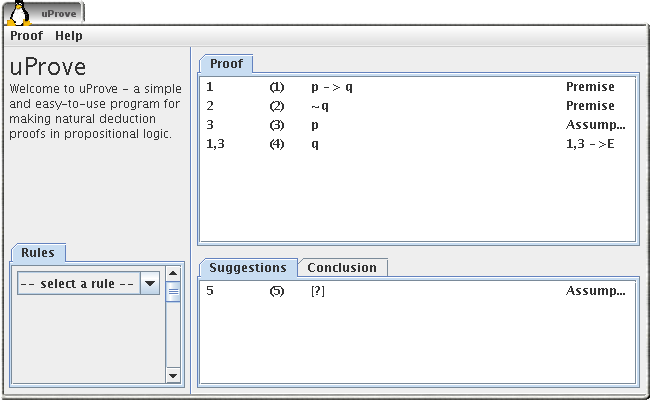
Apply a not elimination
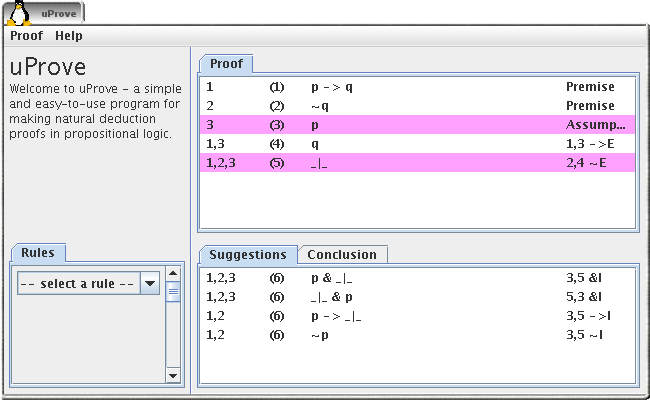
We now have two formulas that clearly contradicts each other. Select these and select the not elimination rule from the list of suggestions.
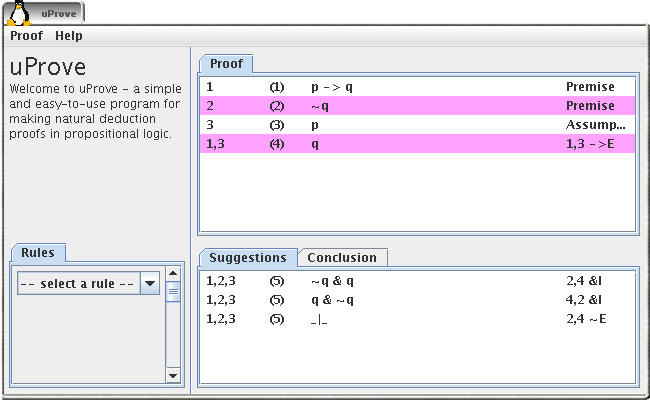
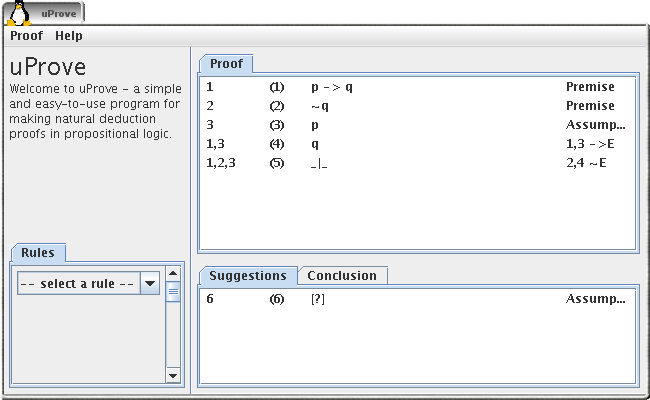
Apply a not introduction
The final step in this proof is applying the not elimination on the assumption and the contradiction. Select these two lines and click on the last line in the list of suggestions.
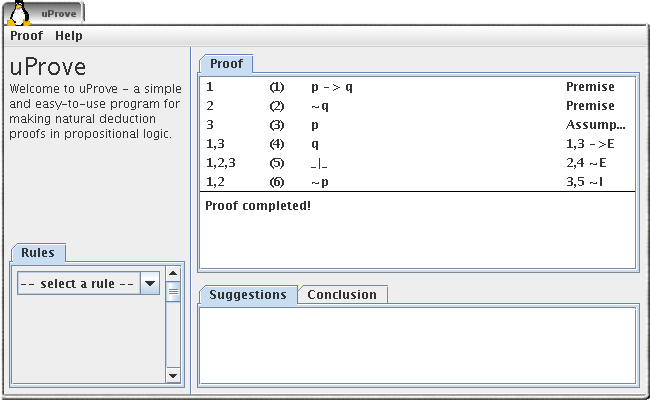
The proof is completed
We have now arrived at a formula which corresponds to the wanted formula, and the last line of the proof does only depend on lines marked as premises. The proof is completed!
Copyright © 2006 Niklas Udd | css | xhtml